Survival analysis, also known as time-to-event analysis, is a statistical methodology used to analyze the duration of time until an event of interest occurs. This powerful tool has wide-ranging applications in various fields, including medicine, engineering, and social sciences. Instead of simply determining whether an event happens or not, survival analysis focuses on when it will occur. By understanding the factors that affect the timing of an event, we can make more accurate predictions and informed decisions.
In this article, we will delve into the basics of survival analysis, its key metrics, data collection methods, and two popular models – the Kaplan-Meier estimator and the Cox proportional hazards model. We will also discuss how to identify and handle censored data, practical applications of survival analysis, and real-world case studies. Finally, we will conclude with best practices and future trends in the field.
Importance of Post-Event Analysis
The study of post-event outcomes is crucial in many domains as it helps to understand and predict the likelihood of certain events occurring. In the medical field, survival analysis is widely used in clinical trials to predict patient survival rates for specific treatments. It is also used to determine the effectiveness of new drugs by analyzing their impact on the duration of time between treatment and mortality.
In engineering, survival analysis is used to analyze the reliability and lifespan of mechanical components. By understanding factors such as stress, wear and tear, and maintenance, engineers can optimize the design and usage of these components. Similarly, in business, survival analysis helps to evaluate the success of marketing campaigns, customer retention rates, and lifetime values. By identifying the key drivers of post-event success, businesses can make strategic decisions to improve their bottom line.
Key Metrics in Survival Analysis
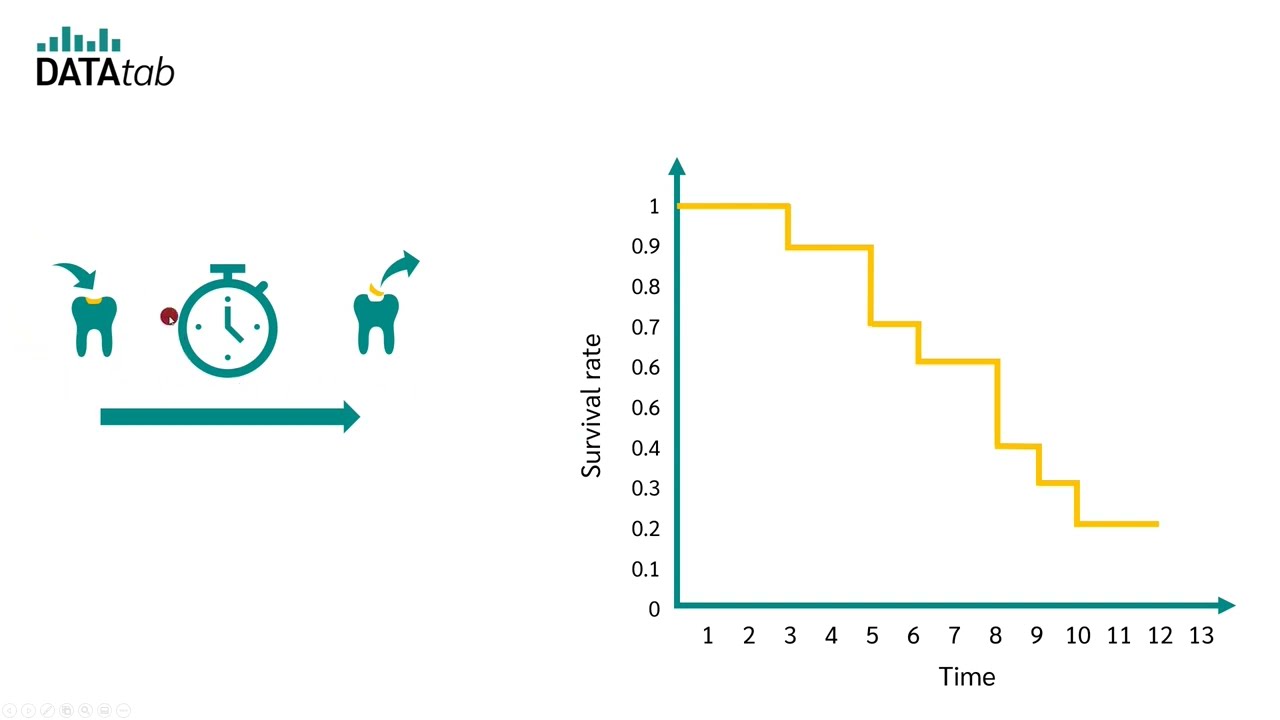
Before diving into the various models and techniques used in survival analysis, it is essential to understand the key metrics that are used to measure the timing of events.
Hazard Rate

The hazard rate, also known as the failure rate, is a fundamental concept in survival analysis. It represents the probability of an event occurring at a specific point in time, given that it has not yet occurred. In other words, it is the instantaneous risk of experiencing the event at any given moment.
Survival Function
The survival function, denoted as S(t), describes the probability of surviving beyond a certain time t. It is defined as the complement of the cumulative distribution function (CDF) and gives us the percentage of individuals who have not yet experienced the event by time t.
Median Survival Time
The median survival time is the time at which 50% of the individuals have experienced the event of interest. It is a useful metric for comparing different groups or treatments.
Data Collection Methods
In survival analysis, data collection methods play a crucial role in obtaining accurate and reliable results. There are two types of data collection methods – prospective and retrospective.
Prospective Data Collection
In prospective data collection, individuals are followed from a specific starting point until the occurrence of the event or the end of the study. This method ensures that all relevant information is recorded, minimizing the risk of bias.
Retrospective Data Collection
Retrospective data collection involves analyzing existing data, such as medical records or historical data, to determine the timing of events. This method is more prone to bias as the data may not have been collected with survival analysis in mind.
Kaplan-Meier Estimator
The Kaplan-Meier estimator is one of the most commonly used non-parametric methods in survival analysis. It is used to estimate the survival function when there are censored data points. The basic formula for the Kaplan-Meier estimator is:

Where ni is the number of individuals who have not yet experienced the event at time ti, and di is the number of events that occur at time ti. This formula takes into account censored data points, which are represented by the term (1 – di/ni). The resulting estimate gives us the probability of survival at each time point, and we can use it to plot a survival curve.
Assumptions of the Kaplan-Meier Estimator
- All individuals in the sample have the same survival chances.
- Censoring is non-informative – the probability of censoring does not depend on the survival time.
Interpreting a Kaplan-Meier Curve

A Kaplan-Meier curve plots the estimated survival function over time. The x-axis represents the time, and the y-axis represents the probability of surviving beyond a specific time. The shaded region around the curve represents the confidence interval, which gives us an idea of the uncertainty in our estimate.
Cox Proportional Hazards Model
The Cox proportional hazards model is a popular semi-parametric model used in survival analysis. Unlike the Kaplan-Meier estimator, this model takes into account the effect of covariates or independent variables on the hazard rate. The basic formula for the Cox proportional hazards model is:

Where h0(t) is the baseline hazard at time t, β is the vector of regression coefficients for the covariates, and x is the vector of covariate values for a particular individual. The model estimates the hazard ratio, which represents the ratio between the hazard rate of two individuals with different covariate values.
Assumptions of the Cox Proportional Hazards Model
- The effect of a particular covariate on the hazard rate is constant over time.
- The baseline hazard is the same for all individuals.
Identifying and Handling Censored Data
As mentioned earlier, censored data is an essential aspect of survival analysis. It occurs when we have incomplete information about the event of interest. There are three types of censoring – right censoring, left censoring, and interval censoring.
Right Censoring
In right censoring, the event has not occurred by the end of the study or a specific cut-off point, and we do not know when it will occur. This type of censoring is commonly seen in clinical trials where patients may be lost to follow-up before the study ends.
Left Censoring
Left censoring occurs when the event has already happened before the study began, and we do not know the exact timing of the event. This type of censoring is common in studies involving historical data.
Interval Censoring
Interval censoring happens when the event occurs within a specific time period, but we do not know the exact time it occurred. This type of censoring is prevalent in epidemiological studies where the onset of disease may be unknown, but we have a range of possible start times.
Practical Applications of Survival Analysis
Survival analysis has a wide range of applications in various fields. Here are some real-world examples:
Clinical Trials
In clinical trials, survival analysis is used to determine the effectiveness of new treatments or drugs by analyzing the time-to-event data of patients. It helps researchers to identify the treatment’s impact on patient survival rates and make informed decisions about its efficacy.
Reliability Engineering
In reliability engineering, survival analysis is used to analyze the time-to-failure of mechanical components. By understanding the factors that affect reliability, engineers can optimize the design and maintenance of these components.
Business Analytics
In business analytics, survival analysis is used to analyze customer retention rates, lifetime values, and marketing campaign effectiveness. By understanding the factors that influence post-event success, businesses can make data-driven decisions to improve their bottom line.
Case Studies and Real-World Examples
Now that we have a good understanding of the concepts and applications of survival analysis, let’s look at some real-world case studies where it has been used successfully.
Clinical Trial for Prostate Cancer Treatment
A study published in the Journal of Clinical Oncology used survival analysis to compare three treatments for prostate cancer – surgery, radiation therapy, and watchful waiting. The study followed 347 patients over a period of 20 years and found that surgery was the most effective treatment in terms of patient survival rates.
Failure Analysis of Aircraft Engines
In a study published in the Journal of Quality Technology, researchers used survival analysis to analyze the failure rates of aircraft engines. The study found that the majority of failures occurred within the first few hundred hours of operation, highlighting the importance of regular maintenance and inspection.
Customer Churn Analysis
In a study by IBM, survival analysis was used to analyze customer churn rates for a telecommunication company. By understanding the factors that influence customer retention, the company was able to identify high-risk customers and take proactive measures to prevent churn.
Best Practices and Future Trends
As with any statistical methodology, there are certain best practices that should be followed when using survival analysis.
- Ensure that the data is collected correctly and free from bias.
- Check for outliers and influential data points before fitting the model.
- Validate the assumptions of the chosen model before making any conclusions.
- Use multiple models and compare the results for robustness.
In recent years, there has been an increase in the use of machine learning techniques in survival analysis, especially in healthcare. These methods can handle large and complex datasets and have the potential to make more accurate predictions. However, it is essential to validate these models before making any decisions based on their results.
Conclusion
Survival analysis is a powerful statistical methodology that allows us to understand the timing of events. Its applications range from predicting patient survival rates to analyzing mechanical component life spans and evaluating marketing campaign effectiveness. With the increasing availability of data and advancements in statistical techniques, survival analysis will continue to play a crucial role in decision-making processes across various industries. By understanding the basics, key metrics, and best practices of survival analysis, we can unlock the secrets of post-event success.

