Use English language, and raw data:
In today’s world, data is constantly being generated at an exponential rate. With the vast amount of information available, it can be overwhelming to uncover meaningful patterns and insights. This is where cluster analysis, a powerful statistical technique, comes into play. By grouping similar data points together, cluster analysis helps to reveal hidden structures and provide valuable insights. It is widely used in various fields such as marketing, healthcare, finance, and environmental science for tasks like customer segmentation, disease diagnosis, outlier detection, and resource allocation. In this article, we will take a deep dive into cluster analysis using the popular programming language R and explore its essential techniques for post-event analysis.
Introduction to Cluster Analysis
Cluster analysis, also known as unsupervised learning, is a statistical method that aims to group data points into clusters based on their similarities. The goal is to create clusters that have high intra-cluster similarity and low inter-cluster similarity, allowing us to identify distinct groups within a dataset. This can help us gain a better understanding of the underlying structure of the data and make more informed decisions.
There are two main types of clustering methods – hierarchical and non-hierarchical. Hierarchical methods create a hierarchy of clusters, whereas non-hierarchical methods directly divide the data into clusters. Each type has its own sub-categories, making it essential to understand the specific needs of your analysis before selecting the appropriate method.
Basics of R Programming for Cluster Analysis
R is a popular open-source programming language and environment for statistical computing and graphics. It provides a wide range of packages and functions for data manipulation, visualization, and modeling, making it a preferred choice for data analysts and researchers. Before diving into cluster analysis, let’s quickly go through some basic concepts of R that will be helpful in our analysis.
Installation and Loading Packages
To install R, one can visit the official website and download the latest version based on their operating system. Once installed, we can open the R console and start our analysis.
R provides various packages for different types of analyses, including cluster analysis. We can install and load a package using the install.packages("package_name") and library(package_name) commands, respectively. For example, to install and load the cluster package, we would use the following commands:
install.packages("cluster")
library(cluster)Data Structures in R
R has various data structures that are used to store and manipulate data. The main ones include vectors, matrices, arrays, data frames, and lists. For cluster analysis, we will primarily be working with data frames, which are similar to tables in a database and allow us to store data of different types. To create a data frame, we can use the data.frame() function, passing in the relevant data as arguments.
# creating a data frame
df <- data.frame(
ID = c(1, 2, 3, 4, 5),
Age = c(25, 30, 40, 35, 28),
Income = c(50000, 60000, 70000, 80000, 75000)
)Data Import and Export
In real-world scenarios, the data is usually stored in external sources like CSV files, Excel spreadsheets, or databases. R provides several functions to import data from these sources into R data frames. Similarly, we can export our results from R to these external sources using relevant functions.
One popular function for importing data is read.csv(), which reads a CSV file and converts it into a data frame. Similarly, for exporting data frames as CSV files, we can use the write.csv() function.
Data Preparation
Before performing any analysis, it is crucial to prepare the data appropriately. For cluster analysis, this involves handling missing values, scaling numeric variables, and converting categorical variables into dummy variables. Let’s go through each step in detail.
Handling Missing Values
Missing values can significantly impact the results of our analysis. Thus, it is crucial to handle them before proceeding. In R, missing values are denoted by NA. We can use the is.na() function to identify missing values in our data frame. There are several ways to handle missing values, including removing rows or columns with missing values, imputing them with mean or median values, or using advanced techniques like multiple imputation.
For our example, we will use the mice package to impute missing values using predictive mean matching (PMM). PMM imputes missing values based on a linear regression model, taking into account relationships among variables. We can install and load the mice package using the following commands:
install.packages("mice")
library(mice)We will then use the mice() function to create multiple imputed datasets, which we can then analyze using our cluster analysis methods.
Scaling Numeric Variables
When working with numeric variables, it is essential to scale them before clustering to avoid any bias towards variables with larger scales. We can use the scale() function in R to standardize our numeric variables, making their means equal to 0 and standard deviations equal to 1.
# scaling numeric variables
df$Age <- scale(df$Age)
df$Income <- scale(df$Income)Dummy Coding Categorical Variables
Categorical variables often require conversion into dummy variables before clustering. This process is known as dummy coding and involves creating binary variables for each unique category in the original variable. For example, if a categorical variable has three categories A, B, and C, it will be converted into three binary variables – A, B, and C, with values 0 or 1 based on the presence of that category in each observation.
In R, we can use the dummy.code() function from the cluster package to convert categorical variables into dummy variables. It is important to note that in hierarchical clustering, the choice of coding scheme for categorical variables does not matter, whereas in non-hierarchical clustering, it can have a significant impact on the results.
# creating dummy variables for categorical variable
dummy_var <- dummy.code(df$Category)Types of Clustering Methods
As mentioned earlier, there are two main types of clustering methods – hierarchical and non-hierarchical. Each type has its own sub-categories, which we will explore in detail below.
Hierarchical Clustering
Hierarchical clustering creates a hierarchy of clusters by iteratively merging or dividing clusters based on their similarity. This process results in a dendrogram, a tree-like diagram that illustrates the relationship between clusters at different levels of the hierarchy. There are two approaches to hierarchical clustering – agglomerative and divisive.
In agglomerative clustering, we start with n clusters, with each cluster containing only one observation. We then iteratively merge clusters that are most similar until we end up with a single cluster. The steps involved in agglomerative hierarchical clustering are as follows:
- Calculate the distance/similarity between each pair of observations using a distance measure like Euclidean or Manhattan distance.
- Group the two closest observations into a cluster.
- Recalculate the distance/similarity between this new cluster and all other clusters.
- Repeat steps 2 and 3 until all observations are combined into a single cluster.
On the other hand, divisive clustering starts with a single cluster containing all observations and iteratively divides it into smaller clusters until we end up with n clusters, with each cluster containing only one observation. The steps involved in divisive hierarchical clustering are as follows:
- Calculate the distance/similarity between each pair of observations using a distance measure like Euclidean or Manhattan distance.
- Divide the entire dataset into two clusters based on some criterion.
- For each of the two derived clusters, repeat step 2 until each cluster contains only one observation.
Hierarchical clustering does not require us to specify the number of clusters beforehand, making it suitable for exploratory analysis. However, it can be computationally expensive and may produce unstable results.
Non-hierarchical Clustering
Non-hierarchical clustering involves directly dividing the data into clusters without creating a hierarchy. There are several methods for non-hierarchical clustering, including k-means, k-medoids, and model-based clustering. Unlike hierarchical clustering, non-hierarchical clustering requires us to specify the number of clusters beforehand.
In k-means clustering, we start by randomly selecting k centroids (center points) from the dataset. We then assign each observation to the nearest centroid, creating k clusters. Next, we recalculate the centroids by taking the mean of all observations in each cluster. We then reassign each observation to the new nearest centroid, and the process repeats until there is no change in the assignments of observations to clusters.
K-medoids clustering is similar to k-means but instead of calculating the mean, it uses the median value of each cluster as the centroid. This makes it more robust to outliers compared to k-means.
Lastly, model-based clustering involves fitting a probability distribution to the data and using it to determine the optimal number of clusters. It is useful when the underlying data distribution is unknown and can handle different shapes of clusters.
Implementing Cluster Analysis in R
Now that we have a basic understanding of the types of clustering methods, let’s explore how to implement them in R. We will be using the cluster package, which provides various functions for clustering and evaluating clusters. For our examples, we will use a simple dataset of customer information, including age, income, and spending habits.
# loading cluster package
library(cluster)
# creating data frame
df <- data.frame(
ID = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10),
Age = c(25, 30, 40, 35, 28, 45, 50, 55, 60, 65),
Income = c(50000, 60000, 70000, 80000, 75000, 90000, 100000, 110000, 120000, 125000),
Spending = c(1000, 2000, 3000, 4000, 3500, 4500, 5000, 5500, 6000, 6500)
)Hierarchical Clustering
To perform hierarchical clustering, we can use the agnes() function. It takes in a distance matrix, which we can calculate using the dist() function. We will use Euclidean distance as our distance measure.
# performing hierarchical clustering
hc <- agnes(dist(df), method = "euclidean")To visualize the results, we can use the plot() function on our hierarchical clustering object.
# plotting dendrogram
plot
From the dendrogram, we can see that the optimal number of clusters could be either 2 or 3. To determine the exact number, we can use the cutree() function, which cuts the dendrogram at a specified height and returns the cluster assignments for each observation.
# cutting dendrogram at height = 5
cutree(hc, h = 5)[1] 1 1 2 2 1 2 2 2 2 2We can see that the observations have been divided into two clusters – one with 5 observations and the other with 5 observations. We can also specify the number of desired clusters using the k argument in the cutree() function.
# cutting dendrogram to obtain 3 clusters
cutree(hc, k = 3)[1] 1 1 2 2 1 2 2 3 3 3Non-hierarchical Clustering
To perform non-hierarchical clustering, we can use the kmeans() function. It takes in the dataset, the number of desired clusters, and the number of times the algorithm will be run (nstart). The latter is important as k-means is sensitive to initial random centroids and running it multiple times can give more reliable results.
# performing k-means clustering with 3 clusters
km <- kmeans(df, centers = 3, nstart = 10)
# cluster assignments
km$cluster[1] 1 1 2 2 2 3 3 3 3 3Similarly, we can perform k-medoids clustering using the pam() function.
# performing k-medoids clustering with 3 clusters
km <- pam(df, k = 3)
# cluster assignments
km$clustering[1] 1 1 2 2 2 3 3 3 3 3Evaluating Clusters
Once we have performed clustering, it is essential to evaluate its performance. This helps us determine the optimal number of clusters and assess the quality of the clusters created. The cluster package provides various functions for evaluating clusters, including silhouette width, Dunn index, and gap statistic.
Silhouette Width
Silhouette width measures how well each observation fits into its assigned cluster. It takes into account both the distance from an observation to other observations within its cluster (a) and the distance from that observation to other observations in the nearest cluster (b). A high silhouette width indicates that the observation is well-matched with its cluster, whereas a low value indicates that it could potentially belong to another cluster.
In R, we can calculate the average silhouette width for our clustering results using the silhouette() function.
# calculating average silhouette width
silhouette(km)Silhouette of 10 units in 3 clusters from pam(x = df, k = 3) :
Cluster sizes and average silhouette widths:
5 3 2
0.594738 0.452286 0.380208We can see that the first cluster has the highest average silhouette width, indicating better cluster cohesion.
Dunn Index
Dunn index is another measure of cluster validity that takes into account both the distances between all clusters (d) and the diameter of each cluster (D). A higher Dunn index indicates better clustering, with a maximum value of 1.
The dunn() function from the cluster package calculates the Dunn index for our clustering results.
# calculating Dunn index
dunn(km) dunn
0.2249281 Gap Statistic
Gap statistic compares the within-cluster dispersion for a given clustering solution with that of a reference distribution generated by random data with similar characteristics as our dataset. The optimal number of clusters is determined based on the value of the gap statistic, with a larger gap indicating a better clustering solution.
In R, we can use the clusGap() function from the cluster package to calculate the gap statistic for our clustering results.
# calculating gap statistic
gap <- clusGap(km)
plot(gap)
From the plot, we can see that the gap statistic increases rapidly until 3 clusters and then starts to level off. This indicates that 3 clusters could be the optimal solution for our data.
Visualizing Clusters
Visualizing the clusters allows us to gain a better understanding of how well the observations are grouped together. In R, we can use various plotting functions to visualize the clusters created using hierarchical and non-hierarchical clustering methods.
For hierarchical clustering, we can plot the dendrogram using the plot() function. Alternatively, we can use the rect.hclust() function, which highlights the clusters on the dendrogram based on the k argument.
# highlighting 3 clusters on the dendrogram
rect.hclust(hc, k = 3)
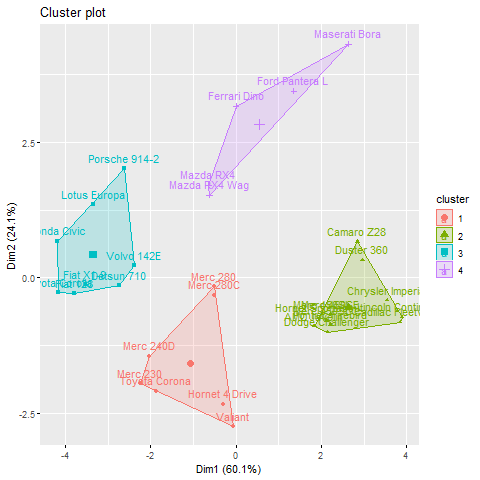
For non-hierarchical clustering, we can use the fviz_cluster() function from the factoextra package, which provides a variety of visualization methods for cluster analysis.
# loading factoextra package
library(factoextra)
# visualizing k-means clusters
fviz_cluster(km, data = df)
The visualization shows the clusters created by the k-means algorithm in a 2-dimensional space, with different colors representing each cluster. This helps us understand the separation and distribution of observations in the feature space.
Practical Applications in Post-Event Analysis
Cluster analysis has numerous practical applications, especially in post-event analysis where we want to group similar entities or events together based on certain attributes or characteristics. Some common applications include customer segmentation, anomaly detection, and pattern recognition.
Customer Segmentation
One of the most prevalent uses of cluster analysis is in customer segmentation, where customers are grouped into distinct segments based on their behavior, preferences, or demographics. By identifying these segments, businesses can tailor their marketing strategies, product offerings, and services to meet the specific needs of each group.
For example, an e-commerce platform might use cluster analysis to segment customers into categories such as frequent buyers, occasional shoppers, and one-time purchasers. This segmentation helps in creating targeted marketing campaigns, personalized recommendations, and loyalty programs to enhance customer engagement and retention.
Anomaly Detection
Cluster analysis can also be employed in anomaly detection, where unusual or unexpected patterns in data are identified as outliers or anomalies. By clustering normal data points together, any observation that does not fit well within a cluster can be flagged as a potential anomaly.
In cybersecurity, for instance, cluster analysis can be used to detect suspicious network activity by grouping normal network behaviors and identifying deviations from these patterns. This helps in detecting cyber threats, intrusions, or malicious activities that deviate from regular network traffic.
Pattern Recognition
Another application of cluster analysis is in pattern recognition, where similarities or patterns in data are identified and labeled accordingly. By clustering data points with similar attributes, patterns within the data can be revealed, leading to insights and actionable strategies.
In bioinformatics, for example, cluster analysis is used to group genes with related functions or expression profiles. By clustering genes based on their expression patterns, researchers can identify gene networks, regulatory pathways, and biological processes underlying specific phenotypes or diseases.
Advanced Techniques and Best Practices
To further enhance the effectiveness of cluster analysis, it is essential to delve into advanced techniques and adhere to best practices that ensure robust and reliable results. Some advanced techniques include feature scaling, dimensionality reduction, ensemble clustering, and consensus clustering.
Feature Scaling
Feature scaling is crucial in cluster analysis, especially when the variables have different scales or units. Normalizing or standardizing the features ensures that each attribute contributes equally to the clustering process, preventing variables with larger scales from dominating the distance calculations.
In R, we can scale our data using the scale() function, which centers and scales the data to have zero mean and unit variance.
# scaling the data
scaled_df <- scale(df)Dimensionality Reduction
Dimensionality reduction techniques like principal component analysis (PCA) or t-distributed stochastic neighbor embedding (t-SNE) can be beneficial in clustering high-dimensional data by reducing the number of features while preserving the essential information. These techniques help in visualizing and interpreting complex datasets, improving the clustering performance.
In R, we can apply PCA using the prcomp() function from the stats package.
# applying PCA
pca <- prcomp(df)Ensemble Clustering
Ensemble clustering involves combining multiple clustering algorithms or multiple runs of the same algorithm to improve the stability and accuracy of the clustering results. By aggregating the individual clusterings, ensemble methods reduce the sensitivity to algorithm parameters and initialization conditions, leading to more robust clusters.
In R, packages like fpc and clValid provide functions for ensemble clustering, such as consensus clustering and cluster validation.
# performing ensemble clustering
ensemble <- consensusClusterPlus(df, maxK = 5, reps = 100)Consensus Clustering
Consensus clustering is a technique that determines the level of agreement among multiple clustering solutions obtained from different algorithms or parameter settings. It helps in identifying stable and reliable clusters by measuring the consensus across various runs, highlighting the robustness of the clustering results.
In R, the ConsensusClusterPlus package offers functions for consensus clustering analysis, providing insights into the optimal number of clusters and the stability of the clusters.
# applying consensus clustering
consensus <- ConsensusClusterPlus(df, maxK = 6, pItem = 0.8, pFeature = 1)Conclusion
In conclusion, cluster analysis is a powerful machine learning technique used to identify inherent structures or patterns within data by grouping similar observations together. In this tutorial, we explored the basics of cluster analysis in R, including different types of clustering methods such as hierarchical and non-hierarchical clustering.
We discussed the importance of data preparation, implementation of clustering algorithms, evaluation of clusters using metrics like silhouette width and Dunn index, and visualization of clusters using dendrograms and scatter plots. We also examined practical applications of cluster analysis in customer segmentation, anomaly detection, and pattern recognition.
Furthermore, we delved into advanced techniques and best practices for enhancing cluster analysis, including feature scaling, dimensionality reduction, ensemble clustering, and consensus clustering. By incorporating these advanced methods, researchers and data scientists can improve the quality and robustness of their clustering results, leading to more meaningful insights and actionable outcomes.
Cluster analysis plays a vital role in various industries and domains, from marketing and finance to healthcare and bioinformatics. By leveraging the versatility and power of cluster analysis in R, analysts can uncover hidden patterns, make informed decisions, and extract valuable knowledge from their data.